viernes, 20 de septiembre de 2013

Ecuaciones cuadráticas

  Una ecuación cuadrática de una variable es una ecuación que tiene la forma de una suma algebraica de términos cuyo grado máximo es dos, es decir, una ecuación cuadrática puede ser representada por un polinomio de segundo grado o polinomio cuadrático. La expresión canónica general de una ecuación cuadrática de una variable es:
ax^2 + bx + c = 0, \quad \mbox{para}\;a\neq 0
donde x representa la variable y a, b y c son constantes; a es un coeficiente cuadrático (distinto de 0), b el coeficiente lineal y c es el término independiente. Este polinomio se puede representar mediante una gráfica de una función cuadrática o parábola. Esta representación gráfica es útil, porque la intersección de esta gráfica con el eje horizontal coinciden con las soluciones de la ecuación (y dado que pueden existir dos, una o ninguna intersección, esos pueden ser los números de soluciones de la ecuación).


File:Ecuación cuadrática.svg
En esta imagen, los puntos comunes de una parábola con el eje X (recta y = 0), las raíces, son las soluciones reales de la ecuación cuadrática.











Fórmula cuadrática

Para una ecuación cuadrática con coeficientes reales o complejos existen siempre dos soluciones, no necesariamente distintas, llamadas raíces, que pueden ser reales o complejas (si los coeficientes son reales y existen dos soluciones no reales, entonces deben ser complejas conjugadas). Se denomina fórmula cuadrática a la ecuación que proporciona las raíces de la ecuación cuadrática:
x = \frac{-b \pm \sqrt {b^2-4ac}}{2a}
donde el símbolo ± indica que los valores
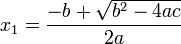
x_1 = \frac{-b + \sqrt {b^2-4ac}}{2a}y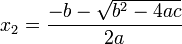\ x_2 = \frac{-b - \sqrt {b^2-4ac}}{2a}
constituyen las dos soluciones.

Ecuaciones cuadráticas disfrazadas

Algunas ecuaciones no parece que sean cuadráticas, pero con manipulaciones astutas se pueden transformar en una:
DisfrazadasQué hacerEn forma estándara, b y c
x2 = 3x -1Mueve todos los términos a la izquierdax2 - 3x + 1 = 0a=1, b=-3, c=1
2(x2 - 2x) = 5Desarrolla paréntesis2x2 - 4x - 5 = 0a=2, b=-4, c=-5
x(x-1) = 3Desarrolla paréntesisx2 - x - 3 = 0a=1, b=-1, c=-3
5 + 1/x - 1/x2 = 0Multiplica por x25x2 + x - 1 = 0a=5, b=1, c=-1

¿Cómo puedo distinguir si es una ecuación cuadrática?

Sólo si se puede poner en la forma ax2 + bx + c = 0, y a no es cero.
El nombre viene de "cuad" que significa cuadrado, así que la mejor pista es que la potencia sea un cuadrado (en otras palabras x2).




Discriminante

En la fórmula anterior, la expresión dentro de la raíz cuadrada recibe el nombre de discriminante de la ecuación cuadrática. Suele representarse con la letra D o bien con el símbolo Δ (delta):

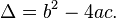
\Delta = b^2 - 4ac.\,

Una ecuación cuadrática con coeficientes reales tiene o bien dos soluciones reales distintas o una sola solución real de multiplicidad 2, o bien dos raíces complejas. El discriminante determina la índole y la cantidad de raíces.
  • Dos soluciones reales y diferentes si el discriminante es positivo (la parábola cruza dos veces el eje de las abscisas: X):
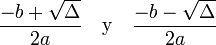\frac{-b + \sqrt {\Delta}}{2a} \quad\text{y}\quad \frac{-b - \sqrt {\Delta}}{2a}.
  • Una solución real doble si el discriminante es cero (la parábola sólo toca en un punto al eje de las abscisas: X):
-\frac{b}{2a} . \,\!
  • Dos números complejos conjugados si el discriminante es negativo (la parábola no corta al eje de las abscisas: X):
\frac{-b}{2a} + i \frac{\sqrt {-\Delta}}{2a}, \quad\text{y}\quad \frac{-b}{2a} - i \frac{\sqrt {-\Delta}}{2a},
donde i es la unidad imaginaria.
En conclusión, las raíces son distintas si el discriminante es no nulo, y son números reales si –sólo si– el discriminante es no negativo.


File:Quadratic equation discriminant.png
Ejemplo del signo del discriminante:
■ < 0: no posee soluciones reales;
■ = 0: posee una solución real (multiplicidad 2);
■ > 0: posee dos soluciones reales distintas.


Para resolver la ecuación cuadrática de la forma ax2 + bx + c = 0 , puede usarse cualquiera de los siguientes métodos:
Solución por factorización
En toda ecuación  cuadrática uno  de sus miembros es un polinomio de segundo grado y el otro es cero; entonces, cuando el polinomio de segundo grado pueda factorizarse, tenemos que convertirlo en un producto de binomios.
Obtenido el producto de binomios, debemos buscar el valor de x de cada uno.
Para hacerlo igualamos a cero cada factor y se despeja para la variable. Igualamos a cero ya que sabemos que si un producto es igual a cero, uno de sus multiplicandos, o ambos, es igual a cero.


Solución por completación de cuadrados
Se llama método de la completación de cuadrados porque se puede completar un cuadrado geométricamente, y porque en la ecuación cuadrática se pueden realizar operaciones algebraicas que la transforman en una ecuación del tipo:
(ax + b)2 = n
en la cual el primer miembro de la ecuación (ax + b)2, es el cuadrado de la suma de un binomio.
Partiendo de una ecuación del tipo
x2 + bx + c = 0


Solución por la fórmula general

Existe una fórmula que permite resolver cualquier ecuación de segundo grado, que es la siguiente:
Ecuacion_Seg_Grado001
La fórmula genera dos respuestas: Una con el signo más (+) y otra con el signo menos (−)  antes de la raíz. Solucionar una ecuación de segundo grado se limita, entonces, a identificar las letras a, b y  c y sustituir sus valores en la fórmula.
La fórmula general para resolver una ecuación de segundo grado sirve para resolver cualquier ecuación de segundo grado, sea completa o incompleta, y obtener buenos resultados tiene que ver con las técnicas de factorización.
  

Trabajando con ecuaciones de segundo grado

Como lo dijimos al comienzo, cualquier ecuación de segundo grado puede, mediante transformaciones, expresarse en la forma ax2 + bx + c = 0,  donde  a,  y  b  son los coeficientes de los términos  x2  y  x, respectivamente y  c es el término independiente.

Ecuación de segundo grado completa

Una ecuación de segundo grado es completa cuando los tres coeficientes  a,  b,  y  c  son distintos de cero.
Entonces, la expresión de una ecuación de segundo grado completa es 
 ax2 + bx + c = 0.

Ecuación de segundo grado incompleta
Una ecuación de segundo grado es incompleta cuando los términos  b  o  c,  o ambos, son cero.
(Si a = 0, la ecuación resultante sería  bx + c = 0,  que no es una ecuación de segundo grado.)
La expresión de una ecuación de segundo grado incompleta es:
ax2 = 0;   si    b = 0    y    c = 0.
ax2 + bx = 0;    si    c = 0.
ax2 + c = 0;    si    b = 0.

CONCLUSIÓN:

Al principio, me imagino que todos tuvimos muchas dificultades!, pero practicando y  resolviendo los problemas con la utilizacion de ecuaciones, te das cuenta que no es tan dificil como lo pensabas. Ese fue mi caso, sentia que ya no podia mas con las ecuaciones, gracias que por fin pude entenderlas, ahora ya no tengo tantos problemas al realizar un problema con las ecuaciones.


Publicado por en

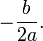
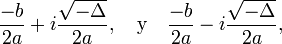
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)